Modelling the proximity effect
When
experimenting with positioning of food items such as small potatoes,
carrots, onions and meatballs in ready meal containers, it is not
uncommon to experience so strong heating in the small contacting
regions of such items that these may dry out or even burn. Two examples
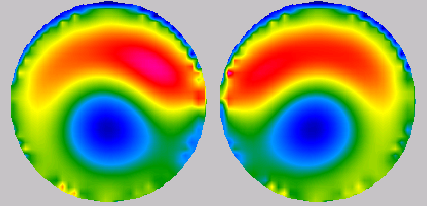
obtained by modelling are shown here. Spherical items with 16 mm
diameter are exposed by a plane wave. The chosen diameter will provide
a compromise between large and small surface areas being close.
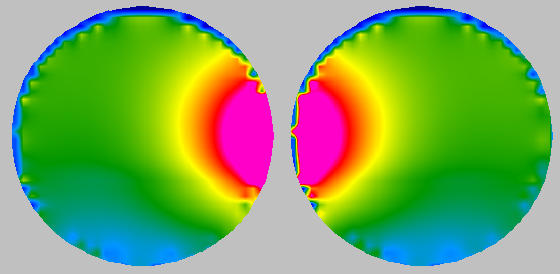
The figures show two examples, with 1 mm distance between spheres with ε =52j20 (left) and 16j4 (right). The
amplitude settings are at the magenta boundaries, and the maximum level
increases with decreasing distance between the items. There
are thus two effects: a general increase of the power density with
closer contact, and a sometimes drastic increase of the power density
in the closest regions.
The
heating in the closest regions must be caused by a concentration of the
displacement current, due to the requirement on its continuity in the
region. Ít can be shown that there is an effective capacitor surface
area of the dielectric bodies in the cases here of about 4×4
mm. The current-carrying capacitance will become almost 8 times smaller
in the airspace than in the bodies with ε
= 52j20 (left images). Thus, a distance in air of only ½ mm has the
same capacitance as 4 mm inside the load. With ½ mm airspace between
the dielectric surfaces there will then very roughly be a comparable
heating effect in the body in general and locally by the additional
capacitive coupling.
If the permittivity ε of
the spheres is instead 16j4 (right images), the coupling phenomena
would occur for larger distances between the items. This is also the
case, as seen in the images.
The capacitance concept with unchanged
capacitor area of the dielectric body would result in only about a
doubling of the distance from the same effect. But a larger part of the
lower- ε bodies participate in the effect as indicated by the size of the affected regions. One may therefore conclude that the
effective coupling distances are approximately inversely proportional
to the permittivity, at least for typical small objects of spherical
shape.
The heating of small regions may become very strong.
They will then dry out and the capacitance will decrease and by that
the effect a negative feedback may occur. Even if burns or Maillard
reaction discolouring may occur, fires will very rarely, if at all,
start by the close contact effect. For that to happen, arcs between
quite sharp edges or points of food substances containing parts with
high fat or sugar content are needed.
It is stated in some
literature that this and other phenomena are caused by an internal
total reflection effect related to the internal standing waves and
resonant patterns. However, the wavelength of the microwaves is
comparable to the characteristic sizes of food items and these are
furthermore so curved that geometric optics concepts are not
applicable. The quasistatic capacitance concept provides sufficient
coupling data for most practical purposes.